階層的クラスタリングをしてみよう
目次
2種類のサンプルデータ
ここでは次のような2種類のデータについて,階層的クラスタリングを行ってみよう.1つ目のデータは階層的クラスタリングの特徴を理解するためのデータです.
2つ目のデータは k-means による非階層クラスタリングによって分析したものと同じデータです.
サンプルデータ (1)
モジュールの読み込みとサンプルデータのダウンロード
ここでは,scikit-learn の sklearn.cluster.AgglomerativeClustering を用いたクラスタリングを行います.まずは,必要なモジュールを読み込み,サンプルデータ (clustering-sample-sample.csv) を GitHub のリポジトリから Pandas のデータフレームに読み込んで表示してみます.
モジュールのインポート
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
# 凝縮型の階層的クラスタリング
from sklearn.cluster import AgglomerativeClustering
# デンドログラム(樹形図)の作成
from scipy.cluster.hierarchy import dendrogram
# 高解像度ディスプレイのための設定
from IPython.display import set_matplotlib_formats
# from matplotlib_inline.backend_inline import set_matplotlib_formats # バージョンによってはこちらを有効に
set_matplotlib_formats('retina')
CSV ファイルの読み込み
url = "https://github.com/rinsaka/sample-data-sets/blob/master/clustering-sample-small.csv?raw=true"
df = pd.read_csv(url)
print(df)
ID x y 0 A 1 2 1 B 1 6 2 C 3 4 3 D 7 4 4 E 11 4 5 F 9 6
次に,上と同じ散布図を描いてみます.
散布図の描画
fig, ax = plt.subplots(1, 1, figsize=(6, 6))
ax.scatter(df['x'], df['y'], alpha=0.8, label=f"data")
ax.set_title("data")
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_xlim(0, 12)
ax.set_ylim(0, 12)
# plt.savefig('aggl_cluster_scatter_01.png', dpi=300, facecolor='white')
plt.show()
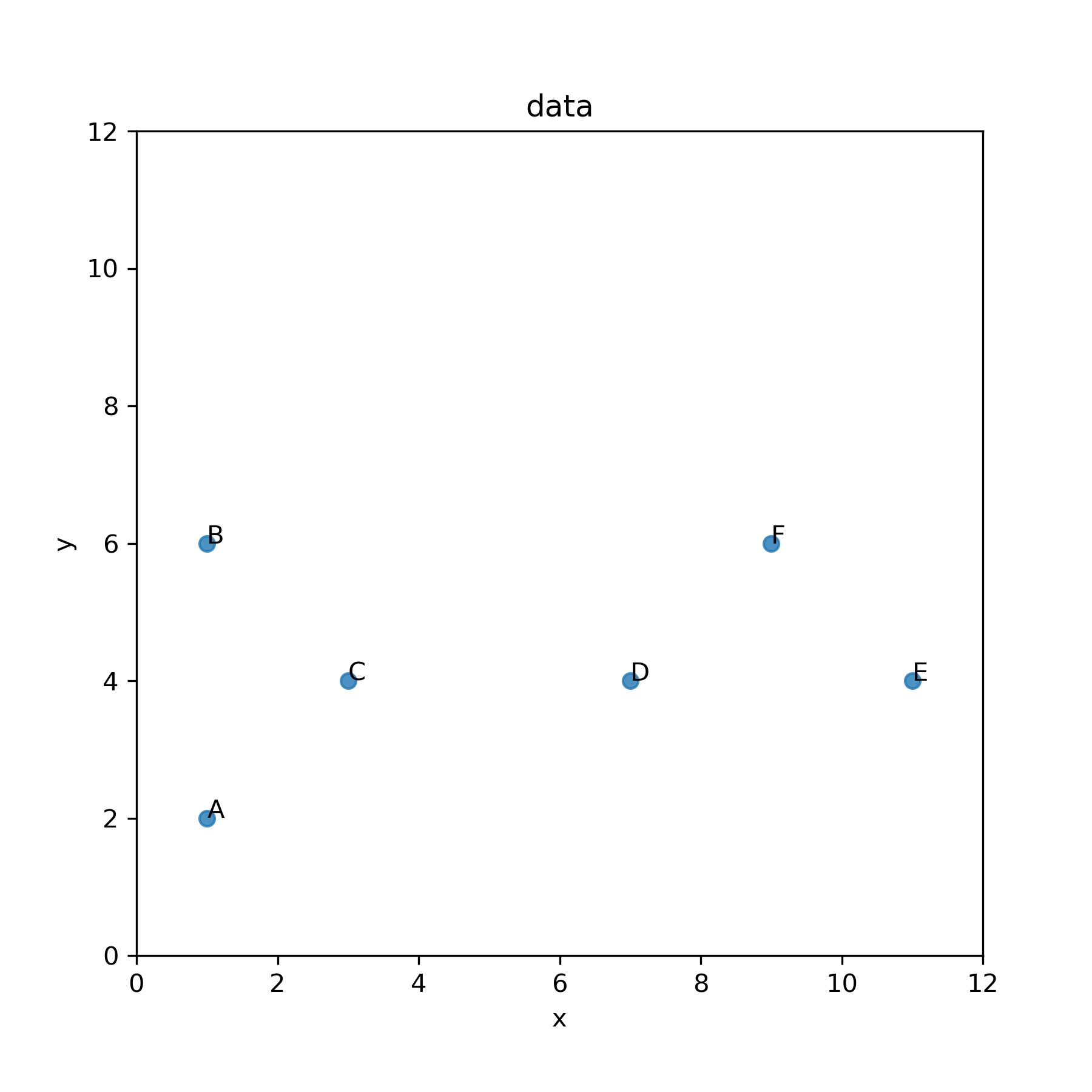
説明の都合上,散布図に ID ラベルを付けてわかりやすくしてみます.
ラベルもプロットする
fig, ax = plt.subplots(1, 1, figsize=(6, 6))
ax.scatter(df['x'], df['y'], alpha=0.8, label=f"data")
ax.set_title("data")
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_xlim(0, 12)
ax.set_ylim(0, 12)
annotations = df['ID'].values
for i, label in enumerate(annotations):
plt.annotate(label, (df['x'][i], df['y'][i]))
# plt.savefig('aggl_cluster_scatter_02.png', dpi=300, facecolor='white')
plt.show()
さらに,個体間の距離がわかりやすいようにグリッドも表示します.
グリッドを表示
fig, ax = plt.subplots(1, 1, figsize=(6, 6))
ax.scatter(df['x'], df['y'], alpha=0.8, label=f"data")
ax.set_title("data")
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_xlim(0, 12)
ax.set_ylim(0, 12)
ax.set_xticks(np.arange(0, 12 + 1, 1))
ax.set_yticks(np.arange(0, 12 + 1, 1))
ax.grid()
annotations = df['ID'].values
for i, label in enumerate(annotations):
plt.annotate(label, (df['x'][i], df['y'][i]))
# plt.savefig('aggl_cluster_scatter_03.png', dpi=300, facecolor='white')
plt.show()
個体間の距離の計算方法
個体間の距離を計算する方法はいくつもあります.代表的な方法は次の通りです.
- ユークリッド距離
- 重み付きユークリッド距離
- マハラノビス距離
- ミンコフスキー距離
このうち,よく用いられるのがユークリッド距離で,2変数の場合は,\((x_{i1},~x_{i2})\) と \((x_{j1},~x_{j2})\) をそれぞれ \(i\) 番目,\(j\) 番目の個体のデータであるとするとき, \begin{eqnarray} d_{ij} &=& \sqrt{\left(x_{i1} - x_{j1}\right)^2 + \left(x_{i2} - x_{j2}\right)^2} \end{eqnarray} となります.一般に \(p\) 個の変数の場合,個体 \((x_{i1},~x_{i2}, \cdots,~x_{ip})\) と \((x_{j1},~x_{j2}, \cdots,~x_{jp})\) のユークリッド距離は \begin{eqnarray} d_{ij} &=& \left|\left| x_{ik} - x_{jk} \right|\right|_2 \\ &=& \sqrt{\sum_{k=1}^{p}\left(x_{ik} - x_{jk}\right)^2} \end{eqnarray} となります.つまり,ユークリッド距離は個体間を直線で結んだ距離になります.なお,ミンコフスキー距離の特別な場合が(詳細は省略しますが,\(q=2\) としたときが)ユークリッド距離になります.また,ユークリッド距離は \(L_2\) ノルムとも呼ばれます.
ユークリッド距離のイメージを掴むために,散布図を描いてみます.
ユークリッド距離
fig, ax = plt.subplots(1, 1, figsize=(6, 6))
ax.scatter(df['x'], df['y'], alpha=0.8, label=f"data")
ax.set_title("Euclidean distance")
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_xlim(0, 12)
ax.set_ylim(0, 12)
ax.set_xticks(np.arange(0, 12 + 1, 1))
ax.set_yticks(np.arange(0, 12 + 1, 1))
ax.grid()
ax.plot(np.array([1, 3]), np.array([2, 4]))
ax.plot(np.array([1, 1]), np.array([2, 6]))
ax.plot(np.array([3, 7]), np.array([4, 4]))
annotations = df['ID'].values
for i, label in enumerate(annotations):
plt.annotate(label, (df['x'][i], df['y'][i]))
# plt.savefig('aggl_cluster_scatter_04.png', dpi=300, facecolor='white')
plt.show()
上の散布図を確認すると,個体間ABや,個体間CDのユークリッド距離は 4 であるのに対して,個体間ACのユークリッド距離は \begin{eqnarray} \sqrt{\left(1 - 3\right)^2 + \left(2 - 4\right)^2} &=& \sqrt{2^2 + 2^2}\\ &=& 2\sqrt{2} \\ &\approx& 2.828 \end{eqnarray} となります.
一方で,ミンコフスキー距離でのもう一つの特別な場合は(詳細は省略しますが,\(q=1\) としたときは)マンハッタン距離になります.マンハッタン距離は市街地距離とも呼ばれ,ニューヨークのマンハッタンや京都市内のように,碁盤の目に区画化された道で測るような距離で,次の式で計算されます. \begin{eqnarray} d_{ij} &=& \left|\left| x_{ik} - x_{jk} \right|\right|_1 \\ &=& \sum_{k=1}^{p} \left| x_{ik} - x_{jk} \right| \end{eqnarray}
なお,マンハッタン距離は \(L_1\) ノルムとも呼ばれます.
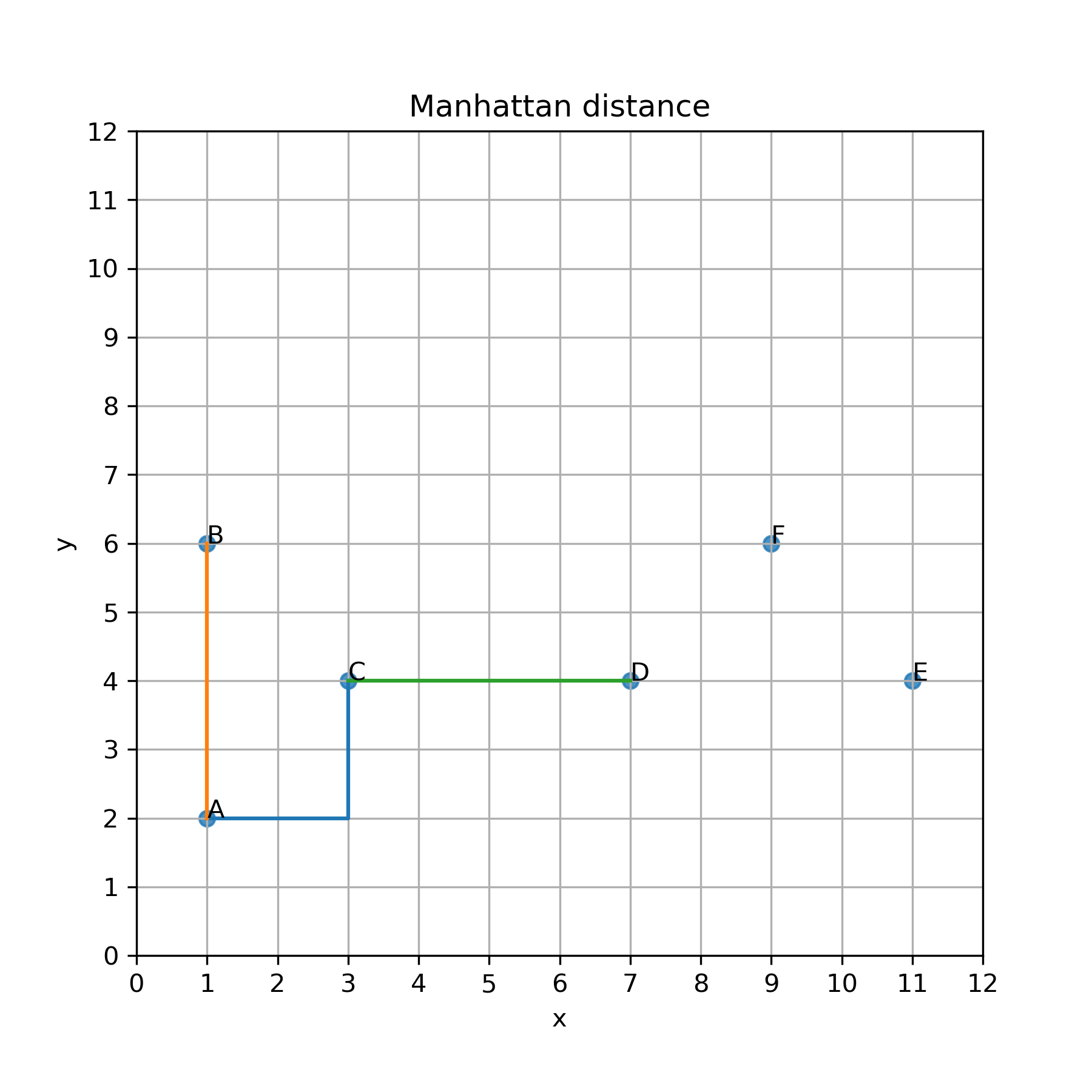
マンハッタン距離のイメージを掴むために,散布図を描いてみます.
マンハッタン距離
fig, ax = plt.subplots(1, 1, figsize=(6, 6))
ax.scatter(df['x'], df['y'], alpha=0.8, label=f"data")
ax.set_title("Manhattan distance")
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_xlim(0, 12)
ax.set_ylim(0, 12)
ax.set_xticks(np.arange(0, 12 + 1, 1))
ax.set_yticks(np.arange(0, 12 + 1, 1))
ax.grid()
ax.plot(np.array([1, 3, 3]), np.array([2, 2, 4]))
ax.plot(np.array([1, 1]), np.array([2, 6]))
ax.plot(np.array([3, 7]), np.array([4, 4]))
annotations = df['ID'].values
for i, label in enumerate(annotations):
plt.annotate(label, (df['x'][i], df['y'][i]))
# plt.savefig('aggl_cluster_scatter_05.png', dpi=300, facecolor='white')
plt.show()
上の散布図から,個体間AB,AC,CDのマンハッタン距離は全て等しく 4 になります.また当然のことながら,個体間ACのマンハッタン距離は次のように計測してもやはり 4 になります.
クラスタ間の距離の計算方法
階層的クラスタリングにおけるデンドログラム(樹形図)の作成過程では,複数の個体をまとめたクラスタ間の距離を決める必要があります.このクラスタ間の距離の計算方法もいくつかあります.ここでは sklearn で利用可能なものだけをリストアップします.
- ウォード法 (ward)
- 群平均法 (average)
- 最長距離法 (complete)
- 最短距離法 (single)
なお,クラスタ間の距離計算にウォード法を用いるときには,個体間の距離計算にユークリッド距離を使う必要があります.
階層的クラスタリングとデンドログラムの作成
ここでは,1つ目のサンプルデータに対して,ユークリッド距離とウォード法を用いて階層的クラスタリングを行い,デンドログラム(樹形図)も作成してみます.
まず,Pandas のデータフレームから必要な列だけを取り出して NumPy 配列に変換します.
xy = df.loc[:, ['x', 'y']].values
print(xy)
[[ 1 2] [ 1 6] [ 3 4] [ 7 4] [11 4] [ 9 6]]
AgglomerativeClustering 関数では個体間距離の計算方法を affinity で指定し、クラスタ間距離の計算方法を linkage で指定します.またここでは,クラスタ数を 2 に設定します.
クラスタリング
num_clusters = 2 # クラスタ数
clustering = AgglomerativeClustering(
n_clusters = num_clusters,
affinity='euclidean', # 個体間の距離はユークリッド距離
linkage='ward', # クラスタ間の距離はウォード法
).fit(xy)
clustering
AgglomerativeClustering()
分類された結果は clustering.labels_ に格納されているので確認します.
clustering.labels_
array([1, 1, 1, 0, 0, 0])
上で確認した結果をデータフレームに cluster_id 列として追加します.
df['cluster_id'] = clustering.labels_
print(df)
ID x y cluster_id 0 A 1 2 1 1 B 1 6 1 2 C 3 4 1 3 D 7 4 0 4 E 11 4 0 5 F 9 6 0
分類された結果を散布図にします.
fig, ax = plt.subplots(1, 1, figsize=(6, 6))
colors = ['Red', 'Blue', 'Green']
for cls in range(num_clusters):
x = df.loc[df['cluster_id'] == cls, 'x']
y = df.loc[df['cluster_id'] == cls, 'y']
ax.scatter(x, y, alpha=0.8, label=f"cluseter {cls}", color=colors[cls])
ax.set_title("Euclidean distance")
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_xlim(0, 12)
ax.set_ylim(0, 12)
ax.set_xticks(np.arange(0, 12 + 1, 1))
ax.set_yticks(np.arange(0, 12 + 1, 1))
ax.grid()
ax.legend(loc='upper left')
annotations = df['ID'].values
for i, label in enumerate(annotations):
plt.annotate(label, (df['x'][i], df['y'][i]))
# plt.savefig('aggl_cluster_scatter_07.png', dpi=300, facecolor='white')
plt.show()
次にデンドログラム(樹形図)を描いてみよう.なお,13, 14, 15 行目のコメント行を有効にすることも可能です.13 行目はフォントサイズの変更,14 行目はデンドログラムを一色で描きます.15 行目はデンドログラムを回転させます.
children = clustering.children_
distance = np.arange(children.shape[0])
no_of_observations = np.arange(2, children.shape[0]+2)
linkage_matrix = np.hstack((
children,
distance[:, np.newaxis],
no_of_observations[:, np.newaxis]
)).astype(float)
fig, ax = plt.subplots(figsize=(6, 6))
dendrogram(
linkage_matrix,
labels= df['ID'].values,
# leaf_font_size=10,
# color_threshold=np.inf,
# orientation='right',
)
ax.set_title("Euclidean distance")
# plt.savefig('aggl_cluster_dendrogram_01.png', dpi=300, facecolor='white')
plt.show()
上のデンドログラムから,個体 A と個体 C の距離が近く最初に結ばれたあと,このクラスタに個体 B が結ばれていることが読み取れます.同様に個体 D と個体 F が結ばれたクラスタに個体 E も連結されていることがわかります.
クラスタリングの結果を確認してみよう.まず,クラスタごとの個体数を確認します.
クラスタごとの個体数
df['cluster_id'].value_counts()
0 3 1 3 Name: cluster_id, dtype: int64
cluster_id が 0 のクラスタについて,x と y の平均値を確認します.
クラスタ 0 の平均値
df[df['cluster_id']==0].mean()
x 9.000000 y 4.666667 cluster_id 0.000000 dtype: float64
クラスタ 1 についても平均値を確認します.
クラスタ 1 の平均値
df[df['cluster_id']==1].mean()
x 1.666667 y 4.000000 cluster_id 1.000000 dtype: float64
デンドログラムの作成で用いた変数について中身を確認しておきます.まず,children です.
children
array([[0, 2],
[3, 5],
[1, 6],
[4, 7],
[8, 9]])
この children の解釈は次のようにすることが可能です.まず,個体 A から F にそれぞれ番号 0 (A), 1 (B), 2 (C), 3 (D), 4 (E), 5 (F) を付与します.children の1行目は [0, 2] であるので,距離が最も近い個体が 0 (A) と 2 (C) となり,この2個体が最初に連結されます(デンドログラムで確認してください).この AC のクラスタに 6 という番号を付与します.children の2行目は [3, 5] であるので,次に距離が近い個体が 3 (D) と 5 (F) となり,この2つが連結され 7 という番号が付与されます.children 3行目は [1, 6] であるので,個体 1 (B) とクラスタ 6 (AC) が次に連結され 8 という番号が付与されます.同じ手順がすべての個体が1つのクラスタに集約されるまで続きます.
次は distance です.これは上の children で各個体(クラスタ)が連結するときの距離を意味します.ただし,計算した距離が格納されているわけでなく,順序が格納されているだけです.
distance
array([0, 1, 2, 3, 4])
次は no_of_observations です.これは children の各手順までに集約された個体数を意味します.
no_of_observations
array([2, 3, 4, 5, 6])
最後に linkage_matrix の中身を確認します.これは,children, distance, no_of_observations を1つの行列にまとめたものです.
linkage_matrix
array([[0., 2., 0., 2.], [3., 5., 1., 3.], [1., 6., 2., 4.], [4., 7., 3., 5.], [8., 9., 4., 6.]])
なお,クラスタリングを実行する際に,compute_distances=True というオプションを付与すると,個体間距離やクラスタ間の距離を計算することができます.このときは,計算結果に clustering.distances_ という属性が含まれるので,distance にこれを指定してデンドログラムを描画することも可能です.
num_clusters = 2 # クラスタ数
clustering = AgglomerativeClustering(
n_clusters = num_clusters,
affinity='euclidean', # 個体間の距離はユークリッド距離
linkage='ward', # クラスタ間の距離はウォード法
compute_distances=True,
).fit(xy)
children = clustering.children_
distance = clustering.distances_
no_of_observations = np.arange(2, children.shape[0]+2)
linkage_matrix = np.hstack((
children,
distance[:, np.newaxis],
no_of_observations[:, np.newaxis]
)).astype(float)
fig, ax = plt.subplots(figsize=(6, 6))
dendrogram(
linkage_matrix,
labels= df['ID'].values,
# leaf_font_size=10,
# color_threshold=np.inf,
# orientation='right',
)
ax.set_title("Euclidean distance")
# plt.savefig('aggl_cluster_dendrogram_01.png', dpi=300, facecolor='white')
plt.show()
print(clustering.distances_)
[ 2.82842712 2.82842712 3.65148372 3.65148372 12.75408431]
この結果 AとCとの距離,およびDとFとの距離が等しく,ともに 2.828 であることなどがわかります.
クラスタ間距離の計算方法を変えてみる
次は個体間の距離計算にマンハッタン距離を使い,クラスタ間の距離計算に様々は方法を用いたときに結果がどのように変化するのかを見てみよう.
群平均法
まずはクラスタ間の距離計算に群平均法を利用してみます.
群平均法
num_clusters = 2 # クラスタ数
clustering = AgglomerativeClustering(
n_clusters=num_clusters,
affinity='manhattan', # 個体間距離はマンハッタン距離
linkage='average', # クラスタ間の距離は群平均法
compute_distances=True,
).fit(xy)
df['cluster_id'] = clustering.labels_
# scatter
fig, ax = plt.subplots(1, 1, figsize=(6, 6))
colors = ['Red', 'Blue', 'Green']
for cls in range(num_clusters):
x = df.loc[df['cluster_id'] == cls, 'x']
y = df.loc[df['cluster_id'] == cls, 'y']
ax.scatter(x, y, alpha=0.5, label=f"cluseter {cls}", color=colors[cls])
ax.set_title("Manhattan distance (average linkage)")
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_xlim(0, 12)
ax.set_ylim(0, 12)
ax.set_xticks(np.arange(0, 12 + 1, 1))
ax.set_yticks(np.arange(0, 12 + 1, 1))
ax.grid()
ax.legend(loc='upper left')
annotations = df['ID'].values
for i, label in enumerate(annotations):
plt.annotate(label, (df['x'][i], df['y'][i]))
# plt.savefig('aggl_cluster_scatter_08.png', dpi=300, facecolor='white')
plt.show()
# dendrogram
children = clustering.children_
distance = np.arange(children.shape[0]) # 順序で樹形図を作成する場合
# distance = clustering.distances_ # 距離で樹形図を作成する場合
no_of_observations = np.arange(2, children.shape[0]+2)
linkage_matrix = np.hstack((
children,
distance[:, np.newaxis],
no_of_observations[:, np.newaxis]
)).astype(float)
fig, ax = plt.subplots(figsize=(6, 6))
dendrogram(
linkage_matrix,
labels= df['ID'].values,
# leaf_font_size=10,
# color_threshold=np.inf,
# orientation='right',
)
ax.set_title("Manhattan distance (average linkage)")
# plt.savefig('aggl_cluster_dendrogram_02.png', dpi=300, facecolor='white')
plt.show()
print(clustering.distances_)

[4. 4. 4. 4. 8.88888889]
マンハッタン距離を用いた場合には,ABが先に結ばれました.これは,AB, ACの距離がどちらも 4 であることから,データの上から順に AB が先に結ばれたものと考えられます.上のコードの34行目をコメントアウトして35行目 distance = clustering.distances_ を有効にすると,異なる結果が得られるはずです.なお,2つのクラスタに分類した散布図の結果はユークリッド距離の場合と一致していることもわかります.
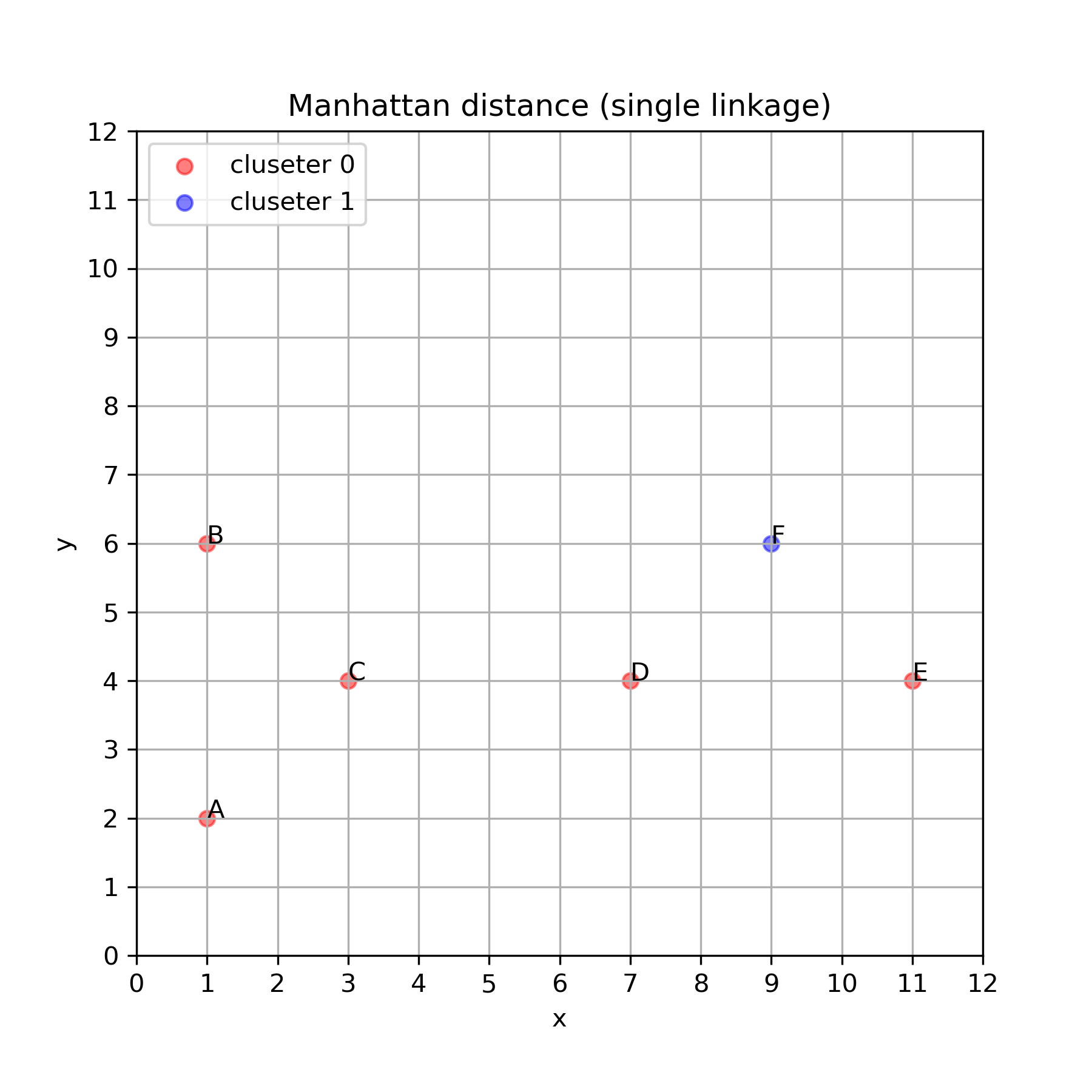
最短距離法
次はクラスタ間の距離計算に最短距離方法用いてみます.
最短距離法
num_clusters = 2 # クラスタ数
clustering = AgglomerativeClustering(
n_clusters=num_clusters,
affinity='manhattan', # 個体間距離はマンハッタン距離
linkage='single', # クラスタ間の距離は最短距離法
compute_distances=True,
).fit(xy)
df['cluster_id'] = clustering.labels_
# scatter
fig, ax = plt.subplots(1, 1, figsize=(6, 6))
colors = ['Red', 'Blue', 'Green']
for cls in range(num_clusters):
x = df.loc[df['cluster_id'] == cls, 'x']
y = df.loc[df['cluster_id'] == cls, 'y']
ax.scatter(x, y, alpha=0.5, label=f"cluseter {cls}", color=colors[cls])
ax.set_title("Manhattan distance (single linkage)")
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_xlim(0, 12)
ax.set_ylim(0, 12)
ax.set_xticks(np.arange(0, 12 + 1, 1))
ax.set_yticks(np.arange(0, 12 + 1, 1))
ax.grid()
ax.legend(loc='upper left')
annotations = df['ID'].values
for i, label in enumerate(annotations):
plt.annotate(label, (df['x'][i], df['y'][i]))
# plt.savefig('aggl_cluster_scatter_09.png', dpi=300, facecolor='white')
plt.show()
# dendrogram
children = clustering.children_
distance = np.arange(children.shape[0]) # 順序で樹形図を作成する場合
# distance = clustering.distances_ # 距離で樹形図を作成する場合
no_of_observations = np.arange(2, children.shape[0]+2)
linkage_matrix = np.hstack((
children,
distance[:, np.newaxis],
no_of_observations[:, np.newaxis]
)).astype(float)
fig, ax = plt.subplots(figsize=(6, 6))
dendrogram(
linkage_matrix,
labels= df['ID'].values,
# leaf_font_size=10,
# color_threshold=np.inf,
# orientation='right',
)
ax.set_title("Manhattan distance (single linkage)")
# plt.savefig('aggl_cluster_dendrogram_03.png', dpi=300, facecolor='white')
plt.show()
print(clustering.distances_)
[4. 4. 4. 4. 4.]
最短距離法では,クラスタ間の最短距離が常に 4 となってしまうことから,連鎖的につながってしまう結果になってしまいました.このデータに対しては分類に失敗していると言えるでしょう.
最長距離法
最後に最長距離法の結果を示します.
num_clusters = 2 # クラスタ数
clustering = AgglomerativeClustering(
n_clusters=num_clusters,
affinity='manhattan', # 個体間距離はマンハッタン距離
linkage='complete', # クラスタ間の距離は最長距離法
compute_distances=True,
).fit(xy)
df['cluster_id'] = clustering.labels_
# scatter
fig, ax = plt.subplots(1, 1, figsize=(6, 6))
colors = ['Red', 'Blue', 'Green']
for cls in range(num_clusters):
x = df.loc[df['cluster_id'] == cls, 'x']
y = df.loc[df['cluster_id'] == cls, 'y']
ax.scatter(x, y, alpha=0.5, label=f"cluseter {cls}", color=colors[cls])
ax.set_title("Manhattan distance (complete linkage)")
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_xlim(0, 12)
ax.set_ylim(0, 12)
ax.set_xticks(np.arange(0, 12 + 1, 1))
ax.set_yticks(np.arange(0, 12 + 1, 1))
ax.grid()
ax.legend(loc='upper left')
annotations = df['ID'].values
for i, label in enumerate(annotations):
plt.annotate(label, (df['x'][i], df['y'][i]))
# plt.savefig('aggl_cluster_scatter_10.png', dpi=300, facecolor='white')
plt.show()
# dendrogram
children = clustering.children_
distance = np.arange(children.shape[0]) # 順序で樹形図を作成する場合
# distance = clustering.distances_ # 距離で樹形図を作成する場合
no_of_observations = np.arange(2, children.shape[0]+2)
linkage_matrix = np.hstack((
children,
distance[:, np.newaxis],
no_of_observations[:, np.newaxis]
)).astype(float)
fig, ax = plt.subplots(figsize=(6, 6))
dendrogram(
linkage_matrix,
labels= df['ID'].values,
# leaf_font_size=10,
# color_threshold=np.inf,
# orientation='right',
)
ax.set_title("Manhattan distance (complete linkage)")
# plt.savefig('aggl_cluster_dendrogram_04.png', dpi=300, facecolor='white')
plt.show()
print(clustering.distances_)
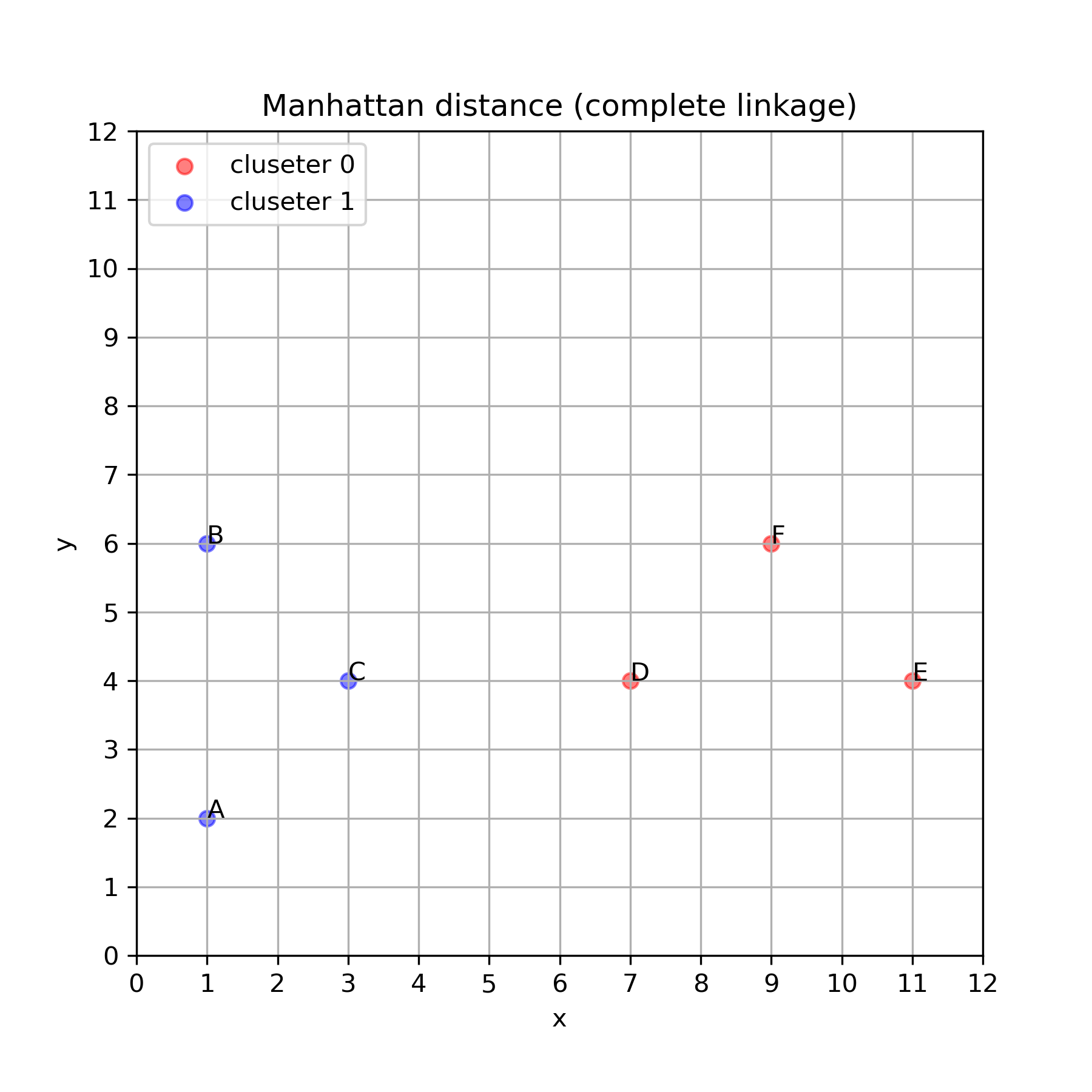
[ 4. 4. 4. 4. 12.]
サンプルデータ (2)
次は,非階層クラスタリングで用いたものと同じデータで階層的クラスタリングを行います.なおユークリッド距離とウォード法を使います.
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
# 凝縮型の階層的クラスタリング
from sklearn.cluster import AgglomerativeClustering
# デンドログラム
from scipy.cluster.hierarchy import dendrogram
from IPython.display import set_matplotlib_formats
# from matplotlib_inline.backend_inline import set_matplotlib_formats # バージョンによってはこちらを有効に
set_matplotlib_formats('retina')
# データの読み込み
url = "https://github.com/rinsaka/sample-data-sets/blob/master/clustering-sample.csv?raw=true"
# url = "clustering-sample.csv" # カレントディレクトリから読み込む場合
df =pd.read_csv(url)
xy = df.loc[:, ['x', 'y']].values
num_clusters = 3 # クラスタ数
clustering = AgglomerativeClustering(
n_clusters = num_clusters,
affinity='euclidean', # 個体間の距離はユークリッド距離を使う
linkage='ward', # クラスタ間の距離はウォード法
).fit(xy)
clustering
df['cluster_id'] = clustering.labels_
fig, ax = plt.subplots(1, 1, figsize=(6, 6))
colors = ['Red', 'Blue', 'Green']
for cls in range(num_clusters):
print()
x = df.loc[df['cluster_id'] == cls, 'x']
y = df.loc[df['cluster_id'] == cls, 'y']
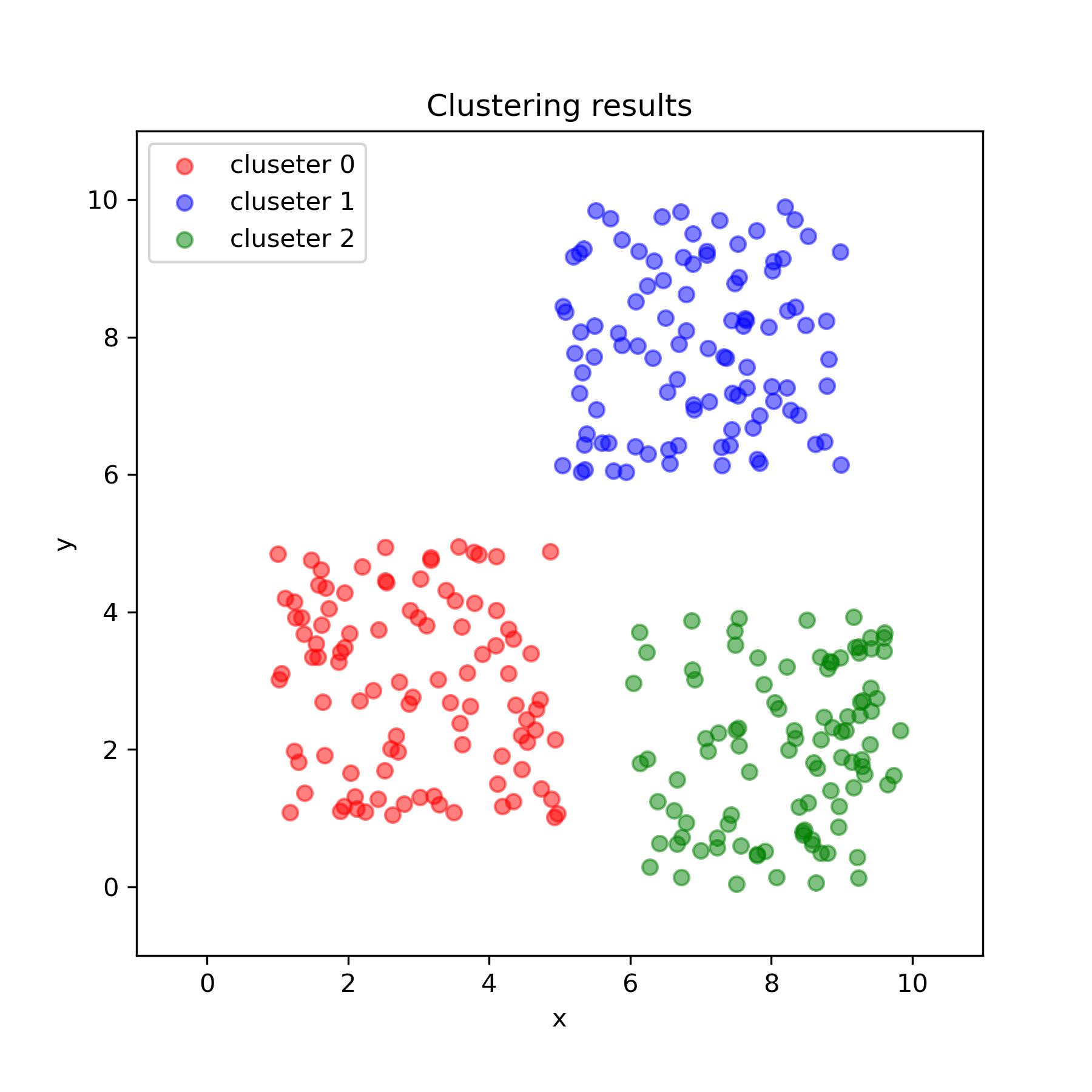
ax.scatter(x, y, alpha=0.5, label=f"cluseter {cls}", color=colors[cls])
ax.set_title("Clustering results")
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_xlim(-1, 11)
ax.set_ylim(-1, 11)
ax.legend(loc='upper left')
# plt.savefig('aggl_cluster_scatter_11.png', dpi=300, facecolor='white')
plt.show()
デンドログラムも作成します.
デンドログラム
children = clustering.children_
distance = np.arange(children.shape[0])
no_of_observations = np.arange(2, children.shape[0]+2)
linkage_matrix = np.hstack((
children,
distance[:, np.newaxis],
no_of_observations[:, np.newaxis]
)).astype(float)
fig, ax = plt.subplots(figsize=(10, 40))
dendrogram(
linkage_matrix,
labels=np.arange(len(xy)),
leaf_font_size=8,
color_threshold=np.inf,
orientation='right',
)
# plt.savefig('aggl_cluster_dendrogram_05.png', dpi=300, facecolor='white')
plt.show()
上のデンドログラムの一部を拡大してみます.71 と 18 の個体が近いことがわかるので,そのデータを表示してみます.
print(df[(df.ID == 71) | (df.ID == 18)])
ID x y cluster_id
18 18 2.5459 4.4306 0
71 71 2.5252 4.4588 0
また,211 と 157 も近いことがわかります.
print(df[(df.ID == 211) | (df.ID == 157)])
ID x y cluster_id 157 157 8.8291 3.2817 2 211 211 8.8474 3.2620 2
55 と 43 が最も近くの個体で,282 は少しだけ離れています.
print(df[(df.ID == 55) | (df.ID == 43) | (df.ID == 282)])
ID x y cluster_id 43 43 7.7957 0.4588 2 55 55 7.8017 0.4752 2 282 282 7.9086 0.5225 2
比較的近い 223 と 52 の距離と, 少し離れた 0 との距離を確認します.
print(df[(df.ID == 223) | (df.ID == 52) | (df.ID == 0)])
ID x y cluster_id 0 0 7.4346 6.6520 1 52 52 7.4170 6.4267 1 223 223 7.2962 6.3995 1