カーネル密度推定をしてみよう

カーネル密度推定 (Kernel Density Estimation／核密度推定，核型密度推定) はノンパラメトリック推定のひとつで教師なし学習に分類されます．データの背後にある真の分布の形状（正規分布や指数分布，ガンマ分布など）を仮定することなく，僅かな数のデータしか得られないような状況でも比較的高精度に確率密度関数を推定でき，データ数が無限大になれば真の確率分布に一致するという特長があります．

ここでは，ある確率分布から得られた10個の標本データ（1.7, 2.5, 2.8, 3.1, 3.4, 3.6, 4.1, 4.4, 6.1, 6.9）をもとにカーネル密度推定を行い，ヒストグラムとその結果を比較します．なお1次元のデータで実行しますが，カーネル密度推定は多次元のデータにも適用可能です．

目次に戻る

ヒストグラム

ヒストグラムはデータの分布を視覚的に捉えることができる最も簡単な方法です．しかしながら，僅かなデータ数しか得られない場合には滑らかなヒストグラムにはなりません．

ヒストグラム
import numpy as np
import matplotlib.pyplot as plt

from IPython.display import set_matplotlib_formats
# from matplotlib_inline.backend_inline import set_matplotlib_formats # バージョンによってはこちらを有効に
set_matplotlib_formats('retina')

a = np.array([1.7, 2.5, 2.8, 3.1, 3.4,3.6, 4.1, 4.4, 6.1, 6.9])
# print(a)

x_min = 0
x_max = 10

fig, ax = plt.subplots(1, 1, figsize=(6, 4))
ax.hist(a, bins=10, range=(x_min, x_max))
plt.savefig('kde-hist.png', dpi=300, facecolor='white')
plt.show()

なお，ヒストグラムを描くときには，階級数の設定に注意する必要があります．上の例では bins=10 によって，階級数を 10 個に設定しました．しかしながら，10個のデータのヒストグラムで10個の階級数は多すぎると思われます．実際にヒストグラムを利用するときには，階級の個数は次のスタージェスの公式を目安に決定すると良いでしょう． \begin{eqnarray} k = 1 + \log_{2} n \end{eqnarray} ここで，\(n\) はデータの個数です．つまり，データの個数 \(n\) が大きくなると，階級数の目安も徐々に増加することになります．例えば，上の \(n = 10\) のデータの場合，スタージェスの公式を用いると階級数の目安は 5 になります．

スタージェスの公式
n = 10
k = 1 + np.log2(n)
k

4.321928094887362

スタージェスの公式によって得られた階級数を使い，さらに階級の上下限も調整してヒストグラムを描きなおします．

ヒストグラム
x_min = 1
x_max = 7
k = 5

fig, ax = plt.subplots(1, 1, figsize=(6, 4))
ax.hist(a, bins=k, range=(x_min, x_max))
plt.savefig('kde-hist5.png', dpi=300, facecolor='white')
plt.show()

目次に戻る

カーネル密度推定

カーネル密度推定は Python の scikit-learn ライブラリで実行できます．まずは，Anaconda Prompt で pip list を実行して「scikit-learn」ライブラリがインストールされていることを確認します．もしもインストールされていなければ pip install scikit-learnでインストールしておく必要があります．

ライブラリのインストールが確認できれば，必要なライブラリをインポートして，標本データを設定します．このとき，n行1列の行列形式に（もしも3次元データの場合はn行3列に）変更する必要があります．

ライブラリの読み込みと標本データの設定
from sklearn.neighbors import KernelDensity
import numpy as np
import matplotlib.pyplot as plt

from IPython.display import set_matplotlib_formats
# from matplotlib_inline.backend_inline import set_matplotlib_formats # バージョンによってはこちらを有効に
set_matplotlib_formats('retina')

a = np.array([1.7, 2.5, 2.8, 3.1, 3.4,3.6, 4.1, 4.4, 6.1, 6.9]).reshape(10,1)
print(a)

[[1.7]
 [2.5]
 [2.8]
 [3.1]
 [3.4]
 [3.6]
 [4.1]
 [4.4]
 [6.1]
 [6.9]]

カーネル関数にはガウスカーネル (gaussian) を指定し，バンド幅には 0.8 を指定してカーネル密度推定による当てはめを行います．

カーネル密度推定による当てはめ
kde = KernelDensity(kernel='gaussian', bandwidth=0.8).fit(a)

横軸に対応する配列を準備したあと，kde.score_samples() で密度関数の値を取得します．ただし，対数で得られることに注意が必要です．

密度関数の値
x_min = 0
x_max = 10
x = np.arange(x_min, x_max, 0.1)
x = x.reshape(x.shape[0], 1) # n行1列の行列に変形

# 密度関数を推定する（対数で得られる）
log_density = kde.score_samples(x)

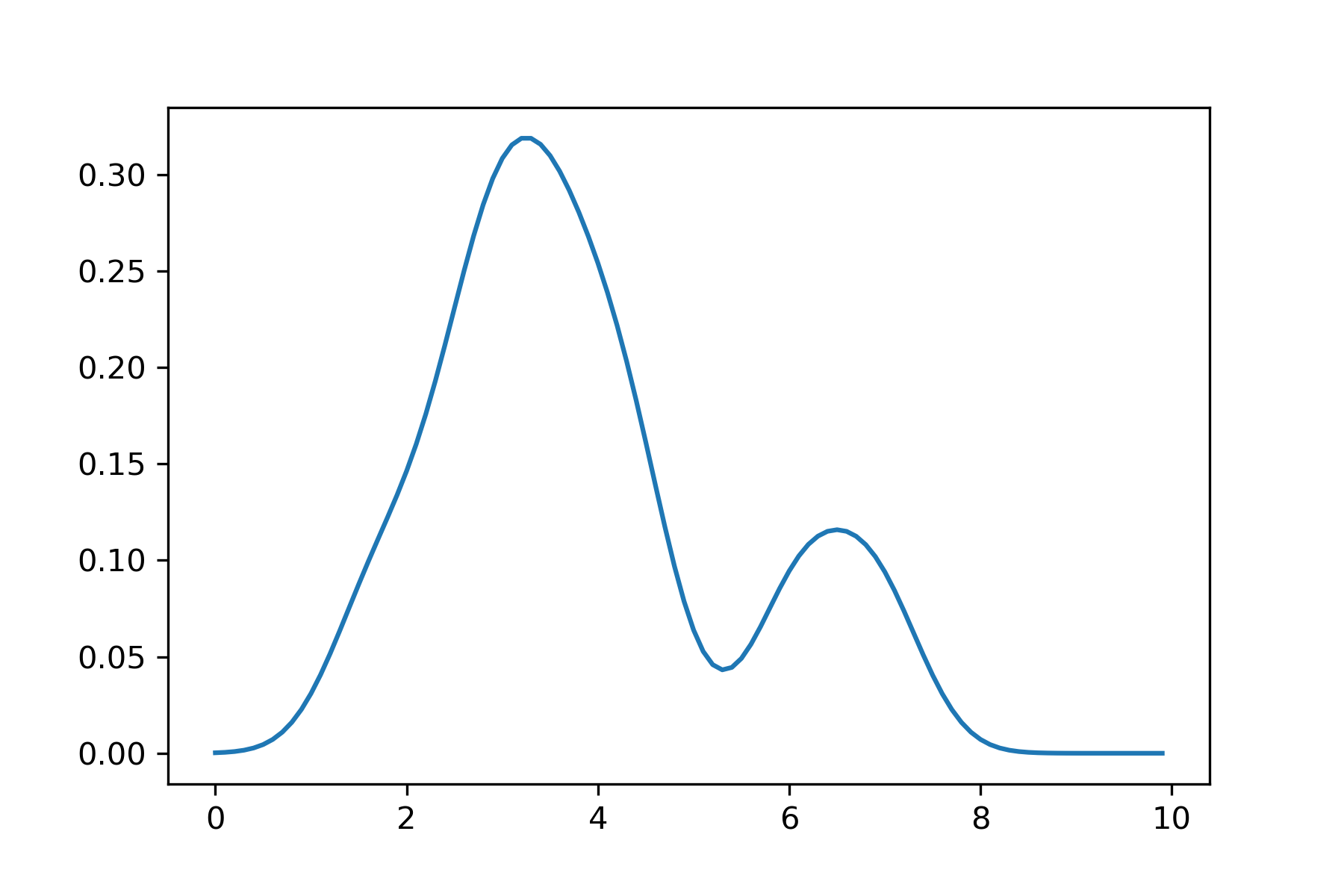
最後に，指数関数を利用して，推定された密度関数をプロットします．わずか10個のデータから滑らかな密度関数を描くことができました．

推定された密度関数のプロット
fig, ax = plt.subplots(1, 1, figsize=(6, 4))
plt.plot(x, np.exp(log_density))
plt.savefig('kde-08.png', dpi=300, facecolor='white')
plt.show()

なお，バンド幅は得られる密度関数の滑らかさに影響するため，慎重に選ぶ必要があります．様々なバンド幅で推定した結果を示します．なお，各図の縦軸スケールは統一していませんが，結果を積分するとどれも1になります．

0.05の場合：

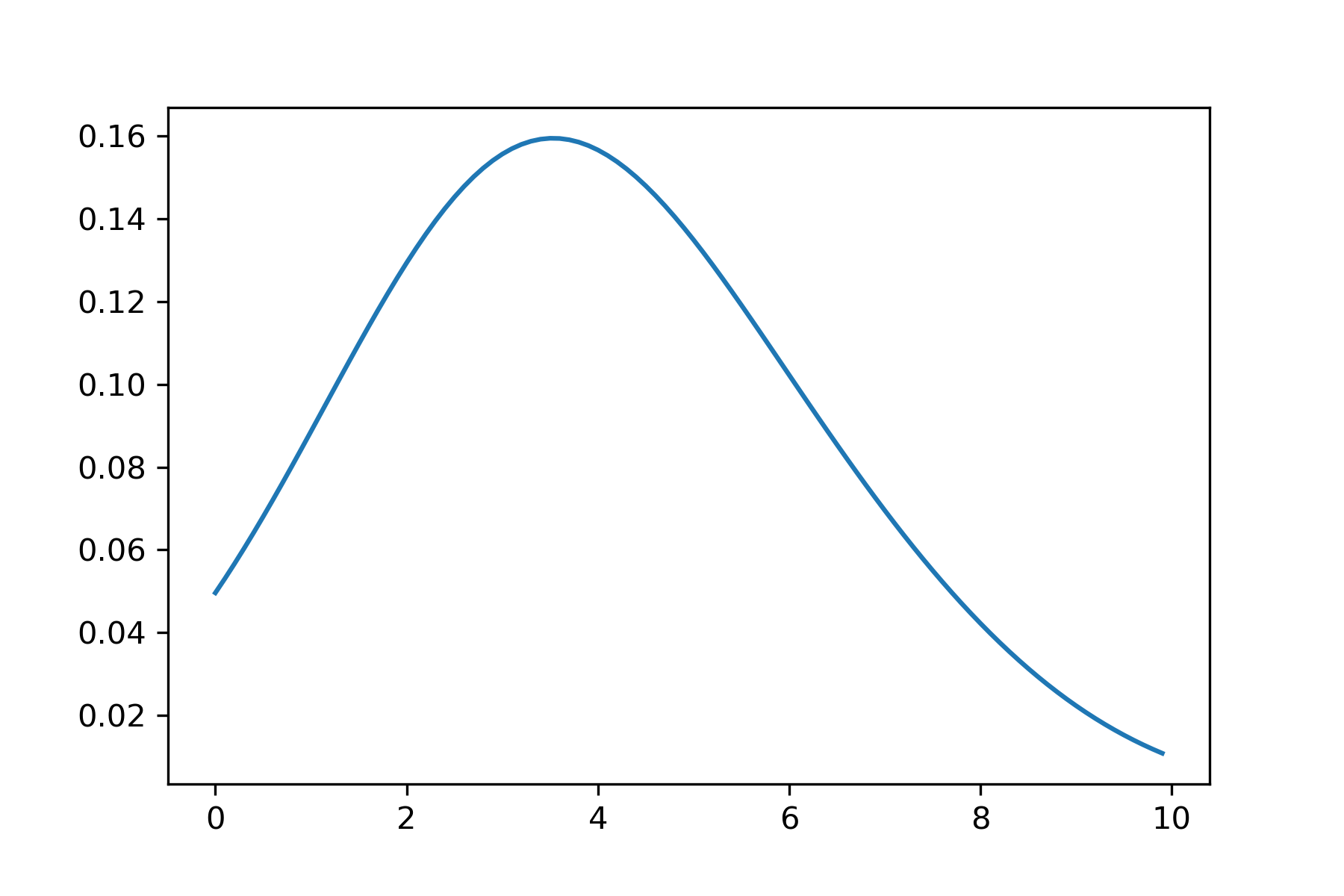
0.1の場合：

0.2の場合：

0.5の場合：

1.0の場合：

2.0の場合：

目次に戻る

カーネル密度推定のしくみ

観測された \(n\) 個のデータ \(x_1, x_2, \cdots, x_n\) が確率密度関数 \(f\) からの標本と仮定します．いまカーネル密度推定量 (kernel density estimator) を次のように定義します． \begin{eqnarray} \hat{f}(y) &=& \frac{1}{nh} \sum_{i=1}^{n} K \left( \frac{y - x_i}{h} \right) \end{eqnarray} ここで，\(h ~(>0)\) はバンド幅 (band width / window size) と呼ばれます．関数 \(K\) はカーネル関数 (kernel function) と呼ばれ次の式を満足するように決定されます． \begin{equation} \int K(t)dt = 1, \quad \int tK(t)dt = 0, \quad \int t^2K(t)dt = r^2 \neq 0 \end{equation} 代表的なカーネル関数はガウスカーネル (Gaussian) \begin{equation} K(t) = \frac{1}{\sqrt{2\pi}} e^{-(1/2)t^2} \end{equation} や，Epanechnikov カーネル \begin{equation} K(t) = \frac{3}{4}\left(1 - \frac{1}{5} t^2 \right) / \sqrt{5} \quad \mbox{ for } |t| > \sqrt{5}, \quad 0 \quad \mbox{ otherwise} \end{equation} です．

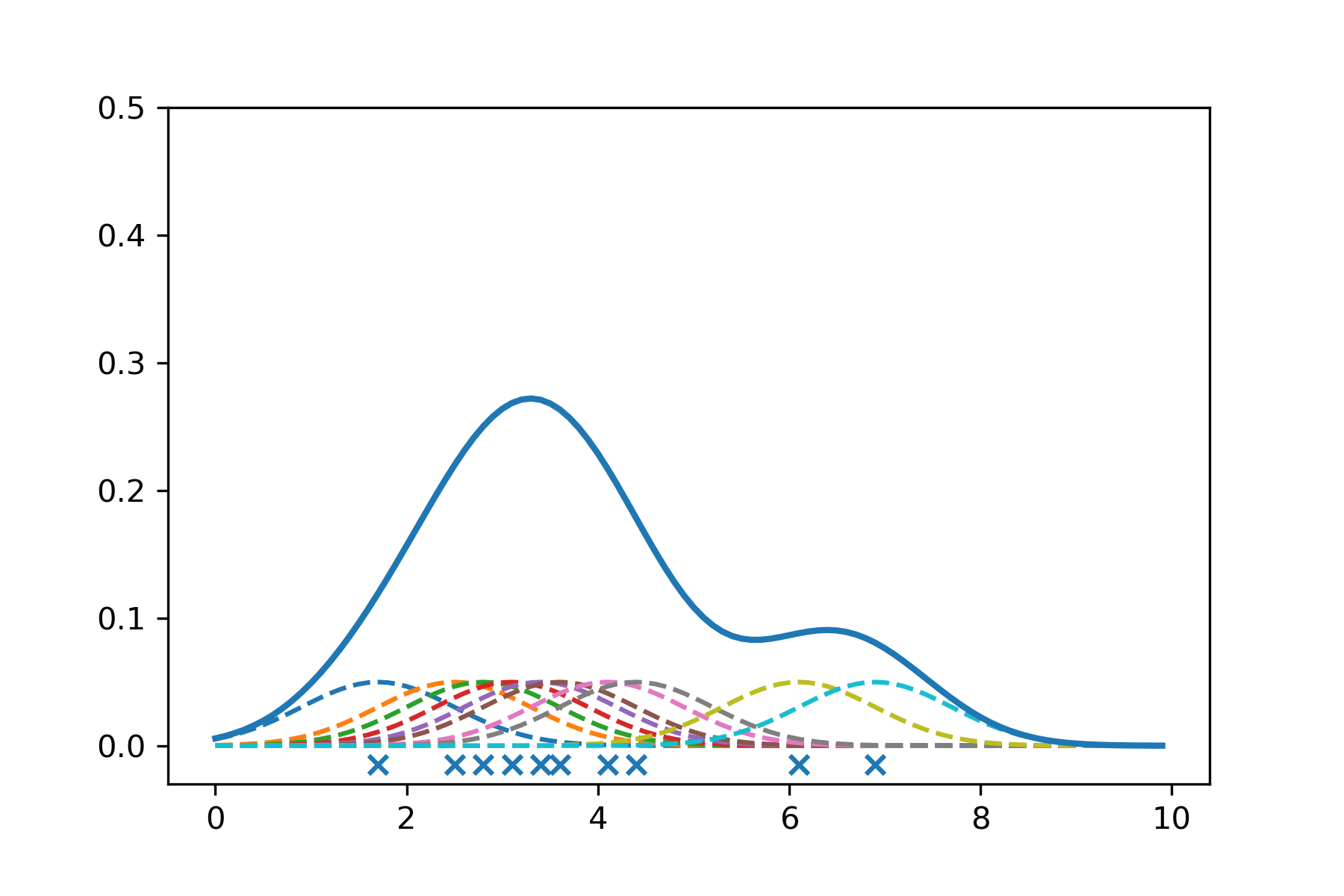
つまり，カーネル密度推定では観測データ一つひとつに対してカーネル関数を用いて「コブ」を作成し，このコブを足し合わせることで密度関数が得られます．次のコードでバンド幅が0.8の場合のコブと密度関数をプロットします．これによりカーネル密度推定のイメージがつかめるはずです．

カーネル密度推定
# バンド幅
h = 0.8

i_max = 10 # データ数
x_min = 0
x_max = 10 # 横軸最大値
y_min = -0.03
y_max = 0.5
x = np.arange(x_min, x_max, 0.1)
x = x.reshape(x.shape[0], 1) # n行1列の行列に変形

# コブを一つひとつ
log_density_kernel = np.zeros((x.shape[0], i_max))
for i in range(0, i_max):
    b = np.array([a[i]])
    kde = KernelDensity(kernel='gaussian', bandwidth=h).fit(b)
    log_density_kernel[:, i] = kde.score_samples(x)

# 密度関数
kde = KernelDensity(kernel='gaussian', bandwidth=h).fit(a)
log_density = kde.score_samples(x)

fig, ax = plt.subplots(1, 1, figsize=(6, 4))
ax.set_ylim(y_min, y_max)

# コブのプロット
for i in range(0, i_max):
    ax.plot(x, np.exp(log_density_kernel[:, i])/10.0, linestyle = "dashed")
# 密度関数のプロット
ax.plot(x, np.exp(log_density), linewidth = 2)
# 標本データのプロット
ax.scatter(a, np.zeros(10)-0.015, marker='x')
plt.savefig('kde-kernel-08.png', dpi=300, facecolor='white')
plt.show()

バンド幅が 0.2 の場合は，（0.8 の場合と比較して）コブ一つひとつの幅が小さく（背が高く）なります．

バンド幅が 1.0 の場合は，（0.8 の場合と比較して）コブ一つひとつの幅が広く（背が低く）なり，その結果，密度関数がより滑らかになります．

また，カーネル関数はコブの形状を決定します．上のコードの16行目と20行目にある 'gaussian' を 'epanechnikov' に変更して実行すると，次のような結果になります（バンド幅は 1.0 としています）．

目次に戻る

参考

カーネル密度推定の利用例や，バンド幅（ウインドウサイズ）の決定方法はこの文献が参考になるかもしれません．また，ガウスカーネルを使う場合は，最適なバンド幅を \begin{eqnarray} h^{*} &=& \left( \frac{4}{3} \right)^{1/5} \sigma n^{-1/5} \\ &\approx& 1.06 \sigma n^{-1/5} \end{eqnarray} を使って求める方法もあります．ここで \(n\) はデータ数，\(\sigma\) は標準偏差です．つまり，データ数 \(n\) が大きくなれば，最適なバンド幅 \(h^{*}\) は徐々に小さくなります．詳細はこの文献で説明しています．

目次に戻る