最短経路問題を解いてみよう
目次
はじめに
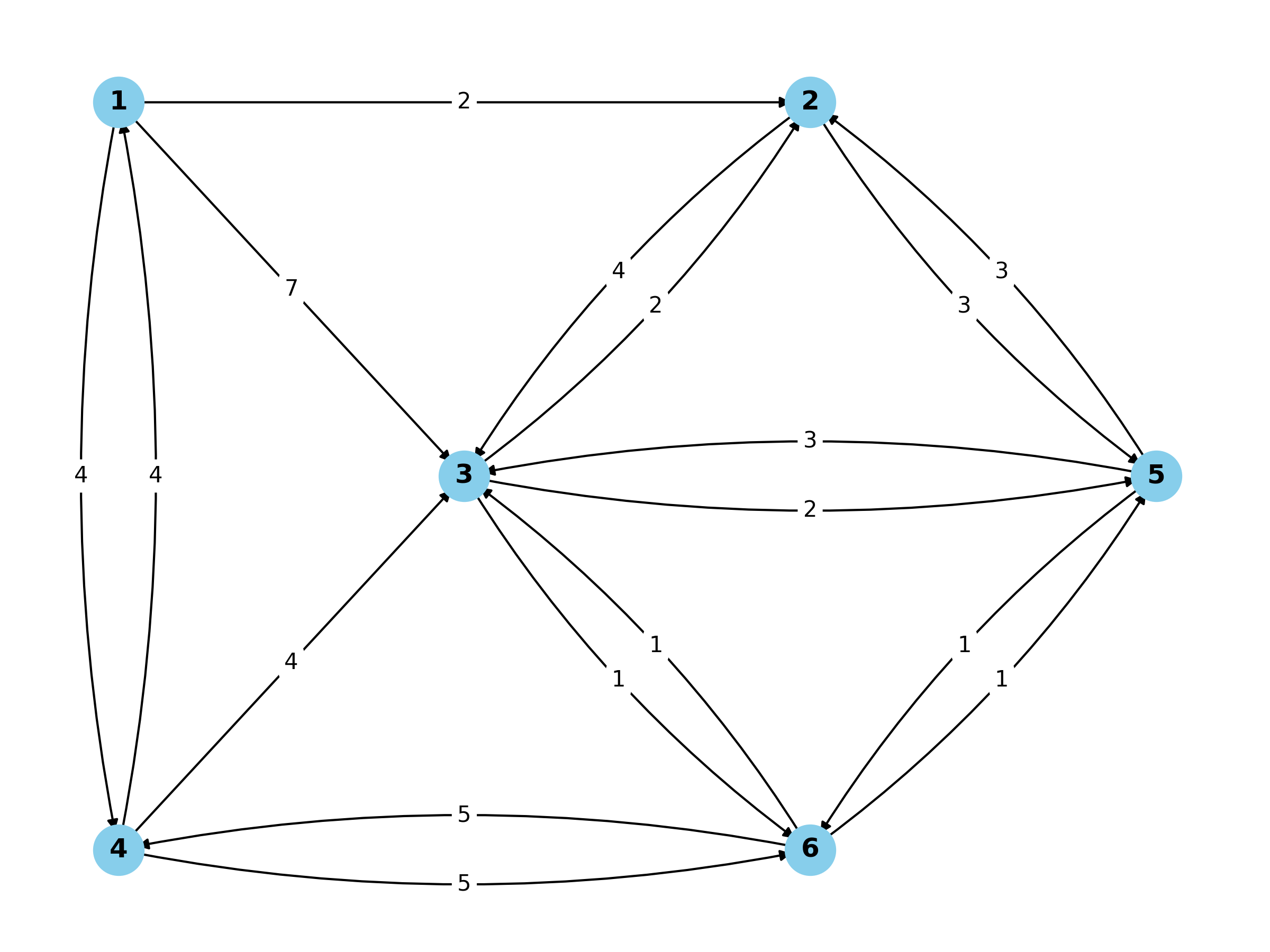
下図のように地点1から地点6のノードがあり,ノード間の移動に必要な時間または距離などの重みが与えられているものとします.例えばノード1から2へは2時間で移動できますが,ノード2から1へは直接移動できません.また,ノード2から3へは移動に4時間を要しますが,逆方向の3から2へは2時間で移動できるとします.このような重み付きグラフにおいて,与えられた2つのノード(例えばノード1からノード6)を結ぶ経路の中で,重みが最小の経路を求める問題を最短経路問題 (shortest path problem) と呼びます.ここでは,Python の NetworkX パッケージを使って,グラフを可視化したり,最短経路を求めたりします.
NetworkX を使ってグラフを作成する
はじめに必要なパッケージをインポートします.データフレームを利用するための pandas,グラフを定義し最短経路問題を解くための networkx,グラフを描画するための matplotlib です.
パッケージのインポート
import pandas as pd
import networkx as nx
import matplotlib.pyplot as plt
次に,ノードの位置データ (nodes.csv) をGitHubから読み込みます.このとき,ローカルにダウンロードしたファイルを読み込んでも構いません.
CSVファイルの読み込み
url_nodes = "https://github.com/rinsaka/sample-data-sets/blob/master/nodes.csv?raw=true"
df_nodes = pd.read_csv(url_nodes)
# df_nodes = pd.read_csv("nodes.csv") # ローカルから読み込む場合
print(df_nodes)
id x y 0 1 1 7 1 2 5 7 2 3 3 4 3 4 1 1 4 5 7 4 5 6 5 1
同じ要領でエッジの重みデータ (edges.csv) を読み込みます.
CSVファイルの読み込み
url_edges = "https://github.com/rinsaka/sample-data-sets/blob/master/edges.csv?raw=true"
df_edges = pd.read_csv(url_edges)
# df_edges = pd.read_csv("edges.csv") # ローカルから読み込む場合
print(df_edges)
node1 node2 weight 0 1 2 2 1 1 3 7 2 1 4 4 3 2 3 4 4 2 5 3 5 3 2 2 6 3 5 2 7 3 6 1 8 4 1 4 9 4 3 4 10 4 6 5 11 5 2 3 12 5 3 3 13 5 6 1 14 6 3 1 15 6 4 5 16 6 5 1
NetworkX を使って有向グラフ (DiGraph) を作成します.なお,NetworkX で利用できるグラフの種類はこちらを参照してください.
有向グラフの作成
G = nx.DiGraph()
いま定義したグラフ (G) に add_node を利用してノードを追加します.Pandasのデータフレームから iterrows() を用いて1行ずつデータを取得してグラフにノードを追加しています.このコードがどのような動作をしているかは,コメントアウトしている print 文を有効化して実行してみると良いでしょう.
ノードの追加(位置情報付き)
for _, row in df_nodes.iterrows():
# print(row)
# print(row['id'], row['x'], row['y'])
G.add_node(row['id'], pos=(row['x'], row['y']))
さらに add_edge を利用してエッジをグラフに追加します.
エッジの追加(重み付き)
for _, row in df_edges.iterrows():
G.add_edge(row['node1'], row['node2'], weight=row['weight'])
定義したグラフがどのようなものか確認します.まず,JupyterLab の自動エコーを利用してグラフ G の内容を表示します.
G
<networkx.classes.digraph.DiGraph at 0x12860b620>
次に print 文を利用して表示します.
print(G)
DiGraph with 6 nodes and 17 edges
クラスの属性値と値を辞書形式で得るためには vars を利用します.
vars(G)
{'graph': {},
'_node': {1: {'pos': (1, 7)},
2: {'pos': (5, 7)},
3: {'pos': (3, 4)},
4: {'pos': (1, 1)},
5: {'pos': (7, 4)},
6: {'pos': (5, 1)}},
'_adj': {1: {2: {'weight': 2}, 3: {'weight': 7}, 4: {'weight': 4}},
2: {3: {'weight': 4}, 5: {'weight': 3}},
3: {2: {'weight': 2}, 5: {'weight': 2}, 6: {'weight': 1}},
4: {1: {'weight': 4}, 3: {'weight': 4}, 6: {'weight': 5}},
5: {2: {'weight': 3}, 3: {'weight': 3}, 6: {'weight': 1}},
6: {3: {'weight': 1}, 4: {'weight': 5}, 5: {'weight': 1}}},
'_succ': {1: {2: {'weight': 2}, 3: {'weight': 7}, 4: {'weight': 4}},
2: {3: {'weight': 4}, 5: {'weight': 3}},
3: {2: {'weight': 2}, 5: {'weight': 2}, 6: {'weight': 1}},
4: {1: {'weight': 4}, 3: {'weight': 4}, 6: {'weight': 5}},
5: {2: {'weight': 3}, 3: {'weight': 3}, 6: {'weight': 1}},
6: {3: {'weight': 1}, 4: {'weight': 5}, 5: {'weight': 1}}},
'_pred': {1: {4: {'weight': 4}},
2: {1: {'weight': 2}, 3: {'weight': 2}, 5: {'weight': 3}},
3: {1: {'weight': 7},
2: {'weight': 4},
4: {'weight': 4},
5: {'weight': 3},
6: {'weight': 1}},
4: {1: {'weight': 4}, 6: {'weight': 5}},
5: {2: {'weight': 3}, 3: {'weight': 2}, 6: {'weight': 1}},
6: {3: {'weight': 1}, 4: {'weight': 5}, 5: {'weight': 1}}},
'__networkx_cache__': {},
'degree': DiDegreeView({1: 4, 2: 5, 3: 8, 4: 5, 5: 6, 6: 6})}
ノードの情報を取得します.
ノードの情報
G._node
{1: {'pos': (1, 7)},
2: {'pos': (5, 7)},
3: {'pos': (3, 4)},
4: {'pos': (1, 1)},
5: {'pos': (7, 4)},
6: {'pos': (5, 1)}}
エッジの情報を取得します.なお,adj は adjacency(隣接)を意味しています.
エッジの情報
G._adj
{1: {2: {'weight': 2}, 3: {'weight': 7}, 4: {'weight': 4}},
2: {3: {'weight': 4}, 5: {'weight': 3}},
3: {2: {'weight': 2}, 5: {'weight': 2}, 6: {'weight': 1}},
4: {1: {'weight': 4}, 3: {'weight': 4}, 6: {'weight': 5}},
5: {2: {'weight': 3}, 3: {'weight': 3}, 6: {'weight': 1}},
6: {3: {'weight': 1}, 4: {'weight': 5}, 5: {'weight': 1}}}
NetworkX にはいくつかの関数もあります.詳細はここで確認してください.まず,ノードを確認します.
ノードの表示
G.nodes()
NodeView((1, 2, 3, 4, 5, 6))
引数 data=True を付与すると次のような結果が得られます.
ノードの表示
G.nodes(data=True)
NodeDataView({1: {'pos': (1, 7)}, 2: {'pos': (5, 7)}, 3: {'pos': (3, 4)}, 4: {'pos': (1, 1)}, 5: {'pos': (7, 4)}, 6: {'pos': (5, 1)}})
ノード数を取得します.
G.number_of_nodes()
6
エッジを確認します.
エッジの表示
G.edges()
OutEdgeView([(1, 2), (1, 3), (1, 4), (2, 3), (2, 5), (3, 2), (3, 5), (3, 6), (4, 1), (4, 3), (4, 6), (5, 2), (5, 3), (5, 6), (6, 3), (6, 4), (6, 5)])
引数 data=True を与えると,次のような結果が得られます.
エッジの表示
G.edges(data=True)
OutEdgeDataView([(1, 2, {'weight': 2}), (1, 3, {'weight': 7}), (1, 4, {'weight': 4}), (2, 3, {'weight': 4}), (2, 5, {'weight': 3}), (3, 2, {'weight': 2}), (3, 5, {'weight': 2}), (3, 6, {'weight': 1}), (4, 1, {'weight': 4}), (4, 3, {'weight': 4}), (4, 6, {'weight': 5}), (5, 2, {'weight': 3}), (5, 3, {'weight': 3}), (5, 6, {'weight': 1}), (6, 3, {'weight': 1}), (6, 4, {'weight': 5}), (6, 5, {'weight': 1})])
エッジの数を確認します.
エッジ数の表示
G.number_of_edges()
17
Matplotlib を使ってグラフを描画する
上で定義したグラフ G を Matplotlib で描画してみます.まず,ノードの位置情報を pos に格納します.なお,get_node_attributes の詳細はこちらで確認してください.
ノードの位置情報取得
pos = nx.get_node_attributes(G, 'pos')
pos
{1: (1, 7), 2: (5, 7), 3: (3, 4), 4: (1, 1), 5: (7, 4), 6: (5, 1)}
内包表記を利用して各エッジに重みのラベルを作成します.
エッジラベルの作成
edge_labels = {(u, v): d['weight'] for u, v, d in G.edges(data=True)}
edge_labels
{(1, 2): 2,
(1, 3): 7,
(1, 4): 4,
(2, 3): 4,
(2, 5): 3,
(3, 2): 2,
(3, 5): 2,
(3, 6): 1,
(4, 1): 4,
(4, 3): 4,
(4, 6): 5,
(5, 2): 3,
(5, 3): 3,
(5, 6): 1,
(6, 3): 1,
(6, 4): 5,
(6, 5): 1}
Matplotlib と NetworkX を用いてグラフを描画します.このとき,双方向エッジは 0.1 の大きさのカーブをつけて描画します.また,エッジラベルもカーブに合わせて位置を調整するようにします.なお,NetworkX の draw_networkx_nodes,draw_networkx_labels,draw_networkx_edges,draw_networkx_edge_labels の詳細はそれぞれのリンクから確認してください.
グラフ描画
plt.figure(figsize=(8, 6))
nx.draw_networkx_nodes(G, pos, node_color='skyblue', node_size=500)
nx.draw_networkx_labels(G, pos, font_size=12, font_weight='bold')
# 双方向エッジにはカーブをつけて描画
arc_rad = 0.1 # カーブの大きさ
for u, v in G.edges():
rad = arc_rad if (v, u) in G.edges() else 0.0 # 双方向エッジはカーブをつける
nx.draw_networkx_edges(
G,
pos,
edgelist=[(u, v)],
connectionstyle=f'arc3,rad={rad}',
arrows=True
)
# エッジラベルの描画(カーブに合わせて調整)
for (u, v), label in edge_labels.items():
rad = arc_rad if (v, u) in G.edges() else 0.0
nx.draw_networkx_edge_labels(
G, pos,
edge_labels={(u, v): label},
label_pos=0.5, # エッジの中央に配置する
font_color='black',
rotate=False, # 文字を回転させない
bbox=dict(facecolor='white', edgecolor='none', boxstyle='round,pad=0.25'),
connectionstyle=f'arc3,rad={rad}'
)
plt.axis('off') # 外の枠線を表示しない
plt.tight_layout() # 上下左右の余白を小さく
# plt.savefig('graph.png', dpi=300, facecolor='white')
plt.show()
最短経路問題を解く
上で定義したグラフに対して NetworkX によって最短経路問題を解きます.次の shortest_pathでは重みを考慮せずに始点1から終点6に至る最短経路を求めています.つまりこれはホップ数が最少となる経路です.
ホップ数最少経路
nx.shortest_path(G, source=1, target=6)
[1, 3, 6]
上で求めた経路のホップ数は shortest_path_length で得ることができます.
ホップ数最少経路のホップ数
nx.shortest_path_length(G, source=1, target=6)
2
ダイクストラ法 (dijkstra_path) によって重みを考慮したいわゆる最短経路問題を解くことができます.
ダイクストラ法による最短経路
nx.dijkstra_path(G, source=1, target=6)
[1, 2, 5, 6]
最短経路の重みの合計(つまり総距離や総時間)を求めるには次の関数 dijkstra_path_length を利用します.
nx.dijkstra_path_length(G, source=1, target=6)
6
上で求めた最短経路を描画してみましょう.もう一度,最短経路を求めてそのパスとエッジを次のようにリスト化します.なお,zip についてはここを参照してください.
始点 1 から終点 6 に至る最短路をダイクストラ法により求める
shortest_path = nx.dijkstra_path(G, source=1, target=6)
shortest_edges = list(zip(shortest_path[:-1], shortest_path[1:]))
print(shortest_path)
print(shortest_edges)
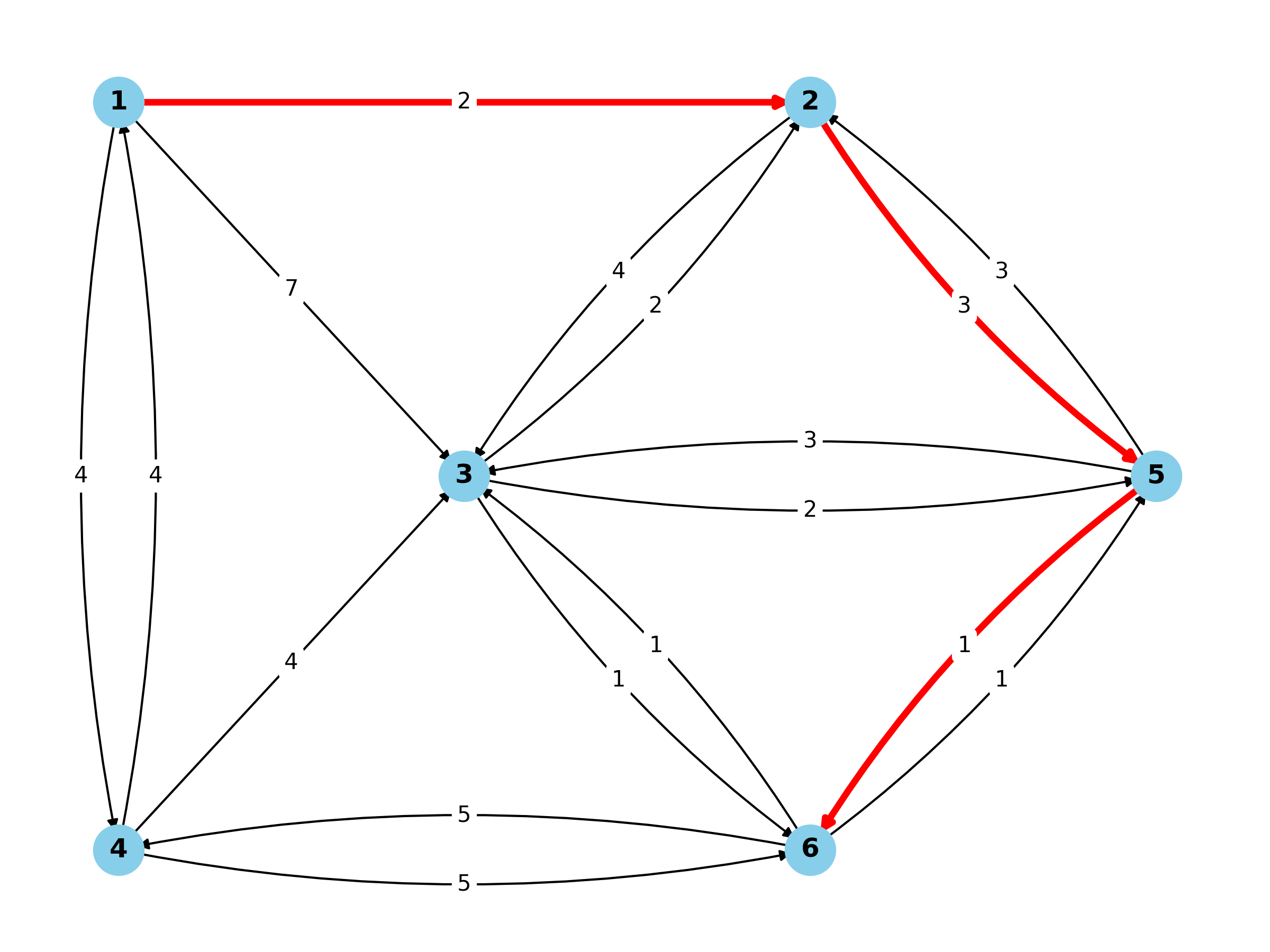
[1, 2, 5, 6] [(1, 2), (2, 5), (5, 6)]
最短路を赤色の太線で描画します.
最短路の描画
plt.figure(figsize=(8, 6))
nx.draw_networkx_nodes(G, pos, node_color='skyblue', node_size=500)
nx.draw_networkx_labels(G, pos, font_size=12, font_weight='bold')
# 双方向エッジにはカーブをつけて描画
arc_rad = 0.1
for u, v in G.edges():
rad = arc_rad if (v, u) in G.edges() else 0.0 # 双方向エッジはカーブをつける
edge_color = 'red' if (u, v) in shortest_edges else 'black' # 最短路であれば赤線に
width = 3 if (u, v) in shortest_edges else 1 # 最短路であれば線幅を3に
nx.draw_networkx_edges(
G,
pos,
edgelist=[(u, v)],
edge_color=edge_color,
connectionstyle=f'arc3,rad={rad}',
arrows=True,
width=width
)
# エッジラベルの描画(カーブに合わせて調整)
for (u, v), label in edge_labels.items():
rad = arc_rad if (v, u) in G.edges() else 0.0
nx.draw_networkx_edge_labels(
G,
pos,
edge_labels={(u, v): label},
label_pos=0.5,
font_color='black',
rotate=False,
bbox=dict(facecolor='white', edgecolor='none', boxstyle='round,pad=0.25'),
connectionstyle=f'arc3,rad={rad}'
)
plt.axis('off')
plt.tight_layout()
# plt.savefig('graph_shortest_path.png', dpi=300, facecolor='white')
plt.show()